Set Operators with Groovy

Donald Raab posted an article about set operators using Java collections and Eclipse Collections. That post focuses on the union, intersection and difference operators. We’ll add in symmetric difference since Groovy supports operator overloading for that operator also.

First, a quick refresh about the operators for two sets A and B:

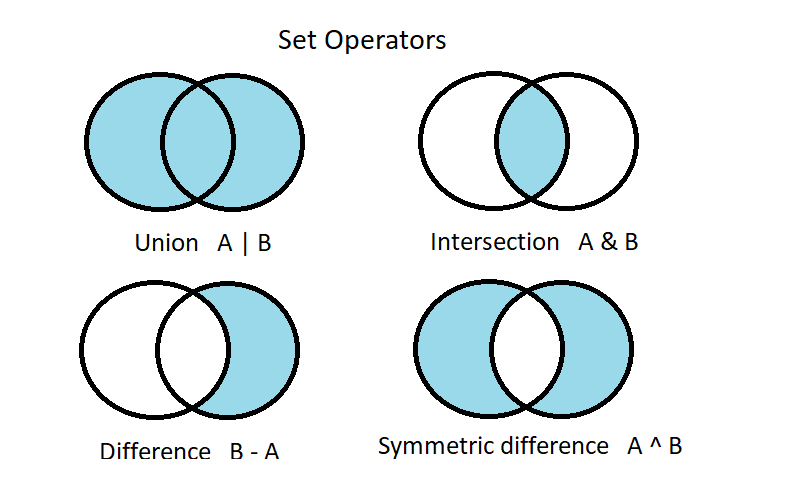
We’ll use the same emoji sets from Donald’s post:

Groovy lets you write the same code as in Donald’s post but also offers operator overloading for these operators as follows:

This code is using standard mutable Java collections, but we could use the normal Set.of(…​) form and work with immutable sets if that was our preference.

Also, since the Eclipse Collections Set implementations implement the standard Java Set interface, these operator overloading shorthands also work when using Eclipse Collections. We simply use Sets.immutable.of(…​) in our set definitions.

What’s more, since Groovy operator overloading is extensible, you can have similar shorthand notation for your own domain objects also. Enjoy!

This example used an alpha version of Groovy 5. Groovy 5 adds a little bit of extra syntactic sugar when using sets. Earlier versions of Groovy have union and intersect methods for sets.